On-Farm Research III: Evaluating Relationships Between Variables

Evaluating relationships between variables involves a statistical method called “regression analysis.”

Last year I wrote two articles on conducting on-farm research. The first explained the basics of experimental design. The second article discussed selection of treatments, randomization and analyzing and interpreting data. As explained in the second article, “analysis of variance” is typically used to compare two or more qualitative treatments, such as type of fertilizers, varieties, rootstocks, dates of application or different growth regulators. Sometimes we are not interested in comparing treatments, but we want to evaluate the relationship between 2 variables, such as number of fruit per tree and the percentage of the fruit in the extra fancy grade. Other times we want to know the optimum concentration of a fertilizer or a growth regulator. For these types of data we typically use a statistical method called “regression analysis” and we can develop an equation to explain the relationship between the two variables and use the equation for future predictions.

Terminology

Terminology is important so we all understand what we are talking about. A predictor variable is the variable that we control; sometimes it is also called the independent variable and is on the horizontal axis of a graph. Examples of predictor variables might include several levels of a fertilizer or growth regulator. We can have several levels of a predictor variable, such as 5 concentrations of NAA or 4 rates of soil-applied nitrogen, or 4 concentrations of herbicide. The variable that we measure, which is affected by the level of the predictor variable is called the response variable or sometimes the dependent variable because the value of the response variable depends on the value of the predictor variable and is on the vertical axis of a graph.

Randomization and replication are important

As with experiments involving qualitative treatments, randomization and replication are very important. Randomization is used to account for varying soil or environmental conditions from one row to the next or from one end of a row to the other. Replication is important to account for the variation among trees and among fruit within trees. Applying a treatment to one section of a block and another treatment to another section of the block may lead to erroneous conclusions because there is no replication or randomization. For most experiments we use a single tree as a replicate, so for most experiments of this type we need at least 15 trees. We try to select trees that are fairly uniform in size, vigor and crop load. The goal is to keep all factors uniform that may affect the response variable except for the predictor variable. In this way we can conclude that the response variable is most likely affected by only the predictor variable.

First select the trees you want to use, and then randomly assign a level of the predictor variable to each tree. An easy way to do this is to select five levels of a variable and write that number on each of three slips of paper. Put the 15 slips in a box and stand in front of one of the trees and select one slip and record the row and tree number along with the level of the predictor variable that will be applied to that tree, so you can find the trees when it is time to apply treatments and record data. Another way to randomize treatments is to obtain 5 colors of flagging (one color for each level of the predictor). Rip three pieces of flagging, each several feet long, off of each role. While looking away, mix the flagging up.

While standing in front of a tree randomly select one piece of flagging and tie it on the tree. We could also use multiple-tree replicates, where we might treat 5 consecutive trees in a row. Remember that these 5 trees are not really replications, but the 5-tree-plot is the replication. In a commercial situation it may be easier to apply a treatment to an entire row of 100 trees. In this case the 100-tree-plot is a single replication, so you will need to apply each level of each treatment to at least 3 rows, but the rows should not be adjacent to each other (randomization). If we were interested in determining the best concentration of NAA to use as a fruit thinner, we might spray an entire row with one concentration and at harvest we could weigh the fruit from that row and divide by the number of trees to estimate average yield per tree.

The appropriate number of replications to use per level of predictor varies with the variability inherit in the response variable. Generally our ability to detect treatment effects increases as the number of replications increases, but there is a point of diminishing returns. If we use more replications than needed, then we waste time and money; if we use too few replications then we may be unable to detect treatment effects. So we try to balance efficiency with the desire to detect treatment effects. When we perform experiments to be analyzed with analysis of variance, we usually prefer to have 6 to 10 replications per treatment. However for regression analysis I prefer to use only 3 or 4 replications so I have enough plant material for at least 5 levels of the treatment (the predictor variables). It is advisable to apply at least 4 and preferably 5 different levels of a predictor variable. When only 3 levels of a predictor variable are used, it is not possible to determine if the response is linear or curved. The levels of the treatment don’t have to be evenly spaced, but there are advantages to using evenly spaced levels; such as 0, 2.5, 5.0, 7.5, and 10.0 ppm of NAA for fruit thinning.

Sampling saves time and money

Measuring all the apples on a tree to determine the average fruit size or measuring all the shoots on a tree to determine average shoot length or counting all the flowers on a tree to determine return bloom is very expensive and not realistic. Although the most reliable data are obtained by measuring every fruit or every shoot on a tree, a reasonable estimate can be obtained by measuring some of the fruit or some of the shoots. This is called “sampling” or “sub-sampling.” The more measurements we make, the closer will be our estimate to the true value. From my experience, measuring at least 20% of the fruit on a tree and about 10% of the shoots on a tree will provide a pretty good estimate of the true average value.

In the case where we simply want to know if there is a relationship between two variables, or if two variables are correlated, we may not have treatments. For example, we may want to know if fruit background color measured with a DA meter is related to starch index for predicting fruit maturity, or we may want to know if average fruit diameter is related to the number of fruit on a tree, or we may want to know if growth of young trees is related to the soil pH around the tree. In this case, with no treatments, we can simply plot the value of one variable (fruit diameter, DA meter value, or tree height) against the other variable (starch index, number of fruit per tree, or soil pH). With Excel software we can easily obtain a best-fit line that will show us the slope of the line.
 

Example of correlation

This summer I wanted to predict apple fruit diameter at harvest from apple diameter measured 60 days after bloom (DAB). I selected 10 representative trees and tagged 10 fruit on each tree. At 60 DAB I measured each fruit with calipers. At harvest time, I again measured each fruit. I entered the values into an Excel spread sheet with one column for fruit diameter 60 DAB and the other column had the diameter of the same fruit at harvest. Table 1 shows an Excel spread sheet with fruit diameters (mm) for five fruit. Column A contains values for fruit diameter at 60 DAB and I called it “diam1”. Column B has diameter values for the same five fruit measured at harvest and I called it “diam2”. A scatter plot of the data can be produced in Excel by highlighting both columns of numbers. Then go to the top of the spreadsheet and click on the “insert” button and then click on the scatter tab. In the drop down menu click on the upper left plot that shows a scatter plot with only markers. You will see a scatter plot of the data and you should be able to tell if there is a pretty good relationship between fruit diameter at 60 DAB and fruit diameter at harvest.

Table 1. Fruit diameter data for 5 fruit in an Excel spread sheet.
 

You can change the range of the values on the axes by right-clicking on one of the numbers on the axis and from the drop down menu choose “format axis.” At the top of the drop down menu click on buttons labeled “fixed” for the minimum and maximum values to adjust the range appropriately. Next click on one of the points in the plot and click on the right side of the mouse. In the drop down menu click on “add trend line.” The new menu will show different types of lines that can be fit to the data. The second option in the list is for a linear trend. In this case, I thought the linear fit would be appropriate.

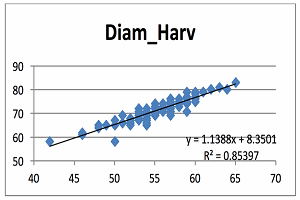
At the bottom of the format trend line box are three boxes. You can check the boxes for “display equation on chart” and “display R-squared value on chart”, then click close. The equation y=1.1388x + 8.3501 appears in the middle of the figure, but for easier reading it can be moved by dragging the box to a section of the plot with no symbols. Below is the figure that I produced. Diameter at harvest (diam2) is on the vertical axis and values range from 50 to 83 mm. The diameter at 60 DAB is on the horizontal axis and the range is 42 to 65 mm. The predicted line goes through the center of the cluster of points.

Interpreting the equation

It is obvious from this plot that there is some variation in the data and the relationship between fruit diameter at 60 DAB and fruit diameter at harvest seems linear. Notice that there were several apples that measured about 54mm at 60 DAB that ranged from 65 to 72cm at harvest. These were big apples because they were ‘Honeycrisp’ from lightly cropped trees. Obviously, all apples do not grow the same. The “y” value in the equation is the predicted value of fruit diameter at harvest. So in English, the equation means that diameter at harvest (mm) is equal to 1.139 times the diameter at 60 DAB plus 8.35mm.

The equation can be used to predict apple fruit diameter at harvest from measurements made at 60 DAB. The intercept is 8.3501 and this means that if an apple had a diameter of zero at 60 DAB, then that apple would have a diameter of 8.3501mm at harvest. Since it is impossible for an apple to have a diameter of zero, we can’t interpret the intercept literally. The slope of the line is 1.1388 and this means the diameter of an apple will increase 1.1388mm for every one mm increase in fruit diameter at 60 DAB.

I hope to be able to use this formula next year to predict the diameter of apples at harvest. Suppose we want to predict the diameter of an apple at harvest when it has a diameter of 55mm at 60 DAB. Using the formula:

Fruit diameter at harvest = (1.139 x 55) + 8.35 = 62.645 + 8.35 = 70.99mm.

So we can expect that fruits with diameters of 55mm at 60 DAB will be about 80mm in diameter at harvest. Don’t try to use this equation next year because I need to repeat the experiment to verify that the slope is similar for the two years.

Interpreting the R2-value

The R2 is called the “coefficient of variation” and is a statistical measure of how close the data are to the fitted line. Another way to think of it is the proportion of the total in fruit diameter at harvest that is explained by the variation in fruit diameter at 60 DAB. R2 values can range from 0 to 1.0; where 0 indicates absolutely no relationship between the two variables and 1.0 means that there is a perfect relationship between the two variables. When R2 is zero, the scatter plot is a cloud of points with no noticeable pattern. When R2 is 1.0, all the points fall exactly on the predicted line. In this example the R2 value of 0.85 means that 85% of the variation in fruit diameter at harvest is explained by variation in fruit diameter 60 DAB. In physics or engineering, researchers often get R2 values of 0.9 or greater. There is a lot of variation in biological data and I rarely see R2 values greater than 0.8 and they are often 0.4 to 0.6, so the R2 value of 0.85 for this data set is pretty good. In general, I feel that if the model doesn’t explain at least half the variation (R2 = 0.5), then the predictive ability of the model isn’t very good.
 

A final word of caution!

It is important to avoid extrapolating beyond your data. In the above example, the largest fruit had a diameter of 65mm at 60 DAB. Since we have no observations of fruit larger than 65mm, we don’t know if the relationship will be the same for larger fruit. It is possible that large fruit might grow at a faster rate or a smaller rate than fruit with diameters of 42 to 65mm.

You can change the range of the values on the axes by right-clicking on one of the numbers on the axis and from the drop down menu choose “format axis.” At the top of the drop down menu click on buttons labeled “fixed” for the minimum and maximum values to adjust the range appropriately. Next click on one of the points in the plot and click on the right side of the mouse. In the drop down menu click on “add trend line.” The new menu will show different types of lines that can be fit to the data. The second option in the list is for a linear trend. In this case, I thought the linear fit would be appropriate.

At the bottom of the format trend line box are three boxes. You can check the boxes for “display equation on chart” and “display R-squared value on chart”, then click close. The equation y=1.1388x + 8.3501 appears in the middle of the figure, but for easier reading it can be moved by dragging the box to a section of the plot with no symbols. Below is the figure that I produced. Diameter at harvest (diam2) is on the vertical axis and values range from 50 to 83 mm. The diameter at 60 DAB is on the horizontal axis and the range is 42 to 65 mm. The predicted line goes through the center of the cluster of points.

Source: psu.edu